Stability
- Will this necessarily be「Bounded Input Bounded Output」?
- Guaranteed if output and hidden activations are bounded
- But will it saturate?
Analyzing Recursion
Sufficient to analyze the behavior of the hidden layer since it carries the relevant information
Assumed linear systems
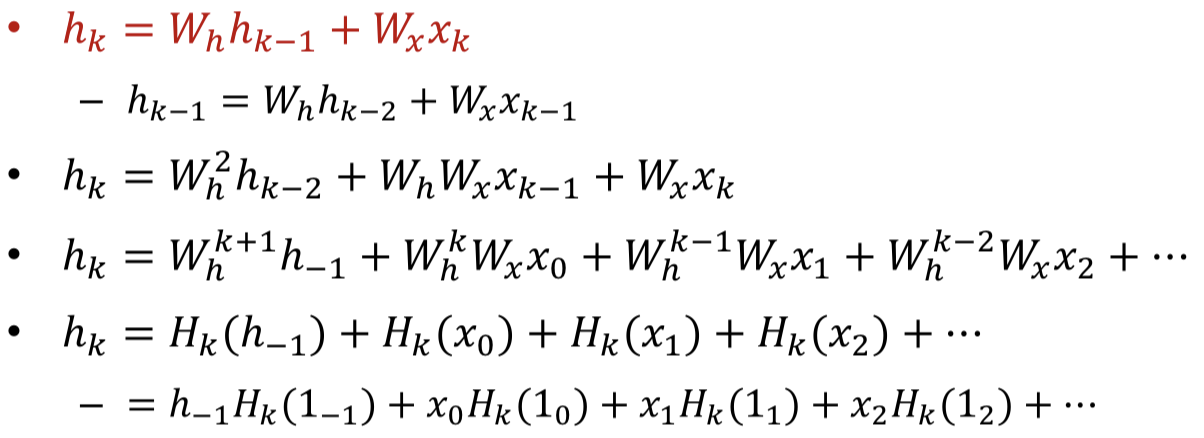
- Sufficient to analyze the response to a single input at (else is zero input)
Simple scalar linear recursion
- If it will blow up
Simple Vector linear recursion
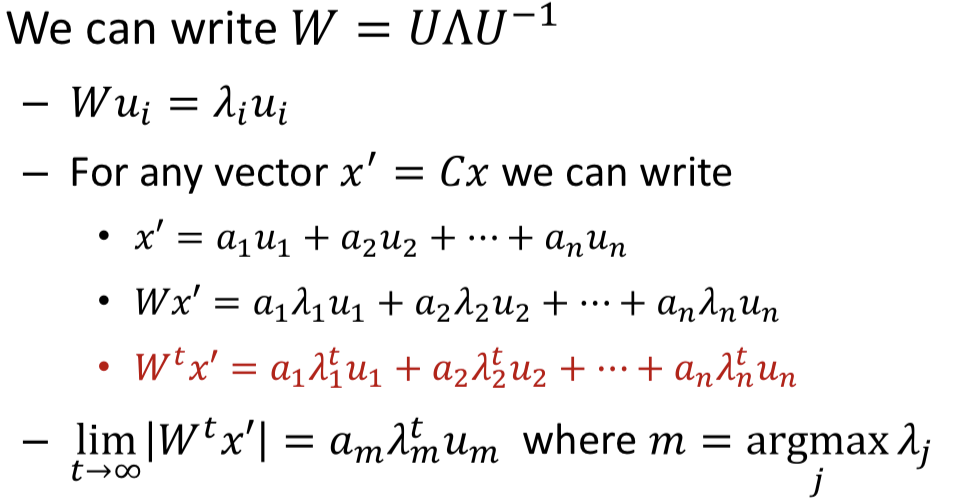
- For any input, for large the length of the hidden vector will expand or contract according to the th power of the largest eigen value of the hidden-layer weight matrix
- If it will blow up, otherwise it will contract and shrink to 0 rapidly
Non-linearities
- Sigmoid: Saturates in a limited number of steps, regardless of
- To a value dependent only on (and bias, if any)
- Rate of saturation depends on
- Tanh: Sensitive to , but eventually saturates
- “Prefers” weights close to 1.0
- Relu: Sensitive to , can blow up
Lessons
- Recurrent networks retain information from the infinite past in principle
- In practice, they tend to blow up or forget
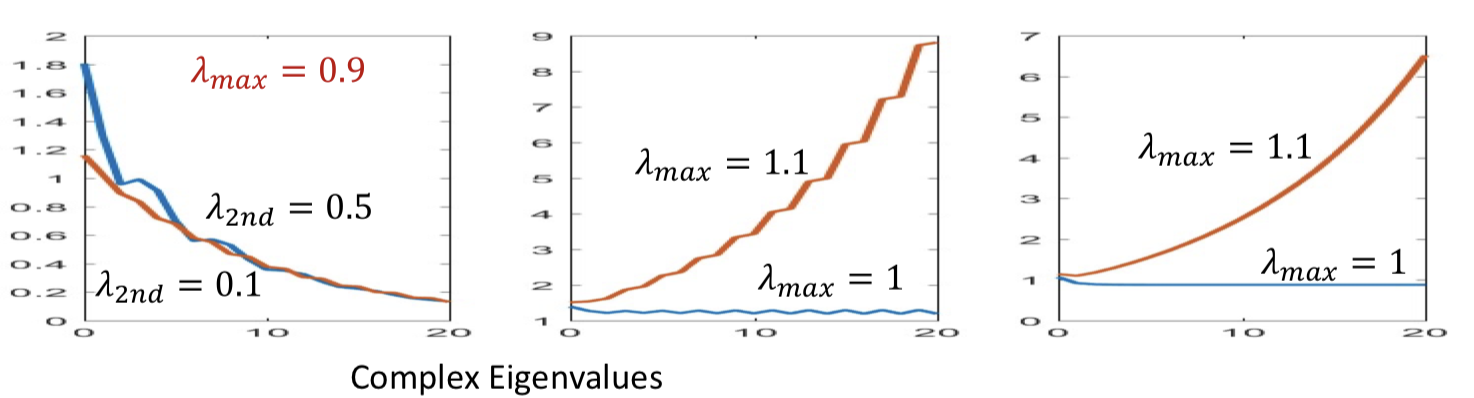
- If the largest Eigen value of the recurrent weights matrix is greater than 1, the network response may blow up
- If it’s less than one, the response dies down very quickly
- The “memory” of the network also depends on the parameters (and activation) of the hidden units
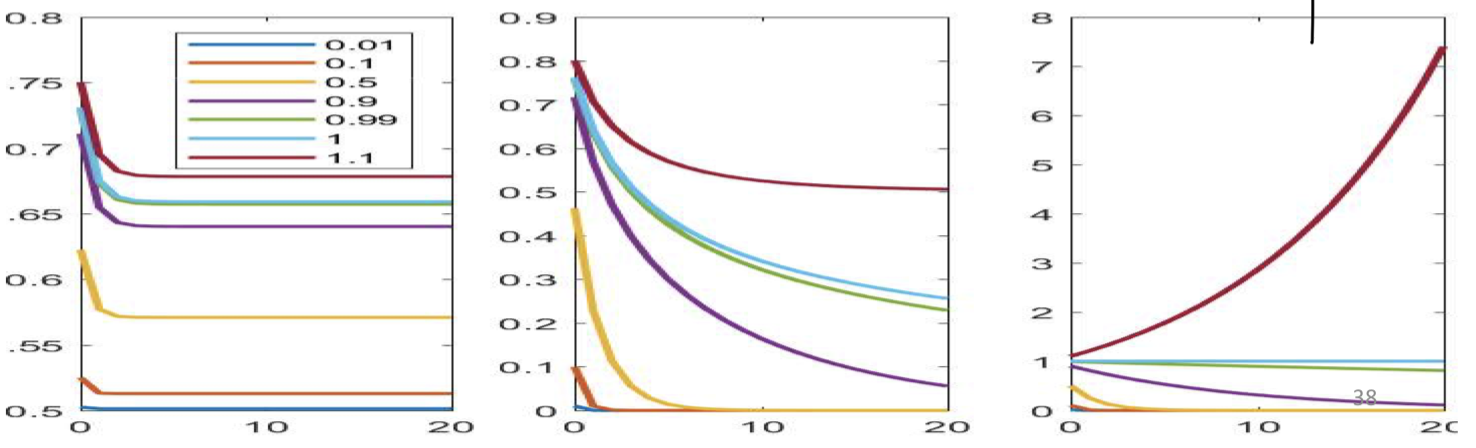
- Sigmoid activations saturate and the network becomes unable to retain new information
- RELU activations blow up or vanish rapidly
- Tanh activations are the most effective at storing memory
- And still has very short “memory”
- Still sensitive to Eigenvalues of
Vanishing gradient
- A particular problem with training deep networks is the gradient of the error with respect to weights is unstable
- For
- We get
- Where
- is jacobian of to its current input
For activation
- For RNN
- For vector activations: A full matrix
- For scalar activations: A matrix where the diagonal entries are the derivatives of the activation of the recurrent hidden layer
- The derivative (or subgradient) of the activation function is always bounded
- Most common activation functions, such as sigmoid, tanh() and RELU have derivatives that are always less than 1
- Multiplication by the Jacobian is always a shrinking operation
- After a few layers the derivative of the divergence at any time is totally “forgotten”
For weights
- In a single-layer RNN, the weight matrices are identical
- The conclusion below holds for any deep network, though
- The chain product for will
- Expand along directions in which the singular values of the weight matrices are greater than 1
- Shrink in directions where the singular values are less than 1
- Repeated multiplication by the weights matrix will result in Exploding or vanishing gradients
LSTM
Problem
- Recurrent nets are very deep nets
- Stuff gets forgotten in the forward pass too
- Each weights matrix and activation can shrink components of the input
- Need the long-term dependency
- The memory retention of the network depends on the behavior of the weights and jacobian
- Which in turn depends on the parameters rather than what it is trying to remember
- We need
- Not be directly dependent on vagaries of network parameters, but rather on input-based determination of whether it must be remembered
- Retain memories until a switch based on the input flags them as ok to forget
- 「Curly brace must remember until curly brace is closed」
- LSTM
- Address the problem of input-dependent memory behavior
Architecture
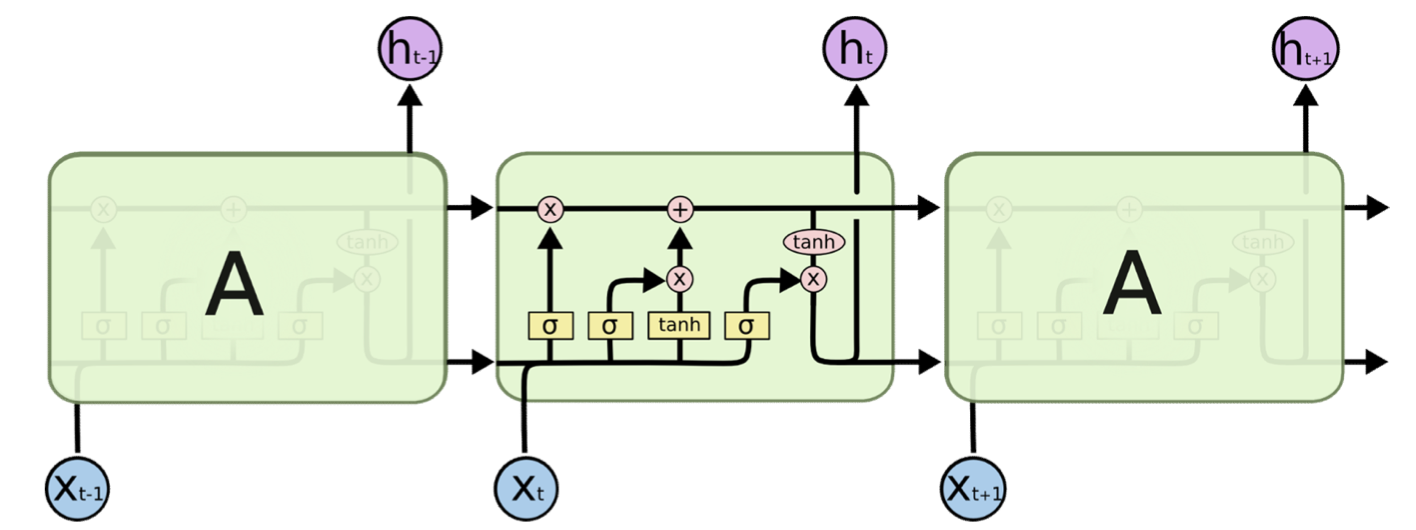
- The are multiplicative gates that decide if something is important or not
Key component
Remembered cell state
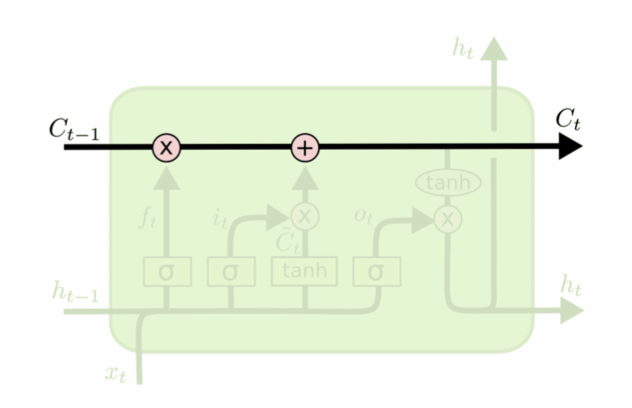
- Mutiply is a switch
- Should I continue remember or not? (scale up / down)
- Acddition
- Should I agument the memory?
- is the linear history carried by the constant-error carousel
- Carries information through, only affected by a gate
- And addition of history, which too is gated..
Gates
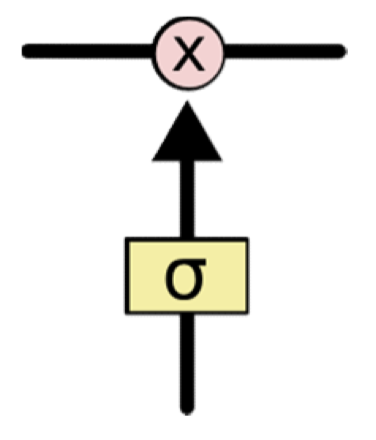
- Gates are simple sigmoidal units with outputs in the range (0,1)
- Controls how much of the information is to be let through
Forget gate
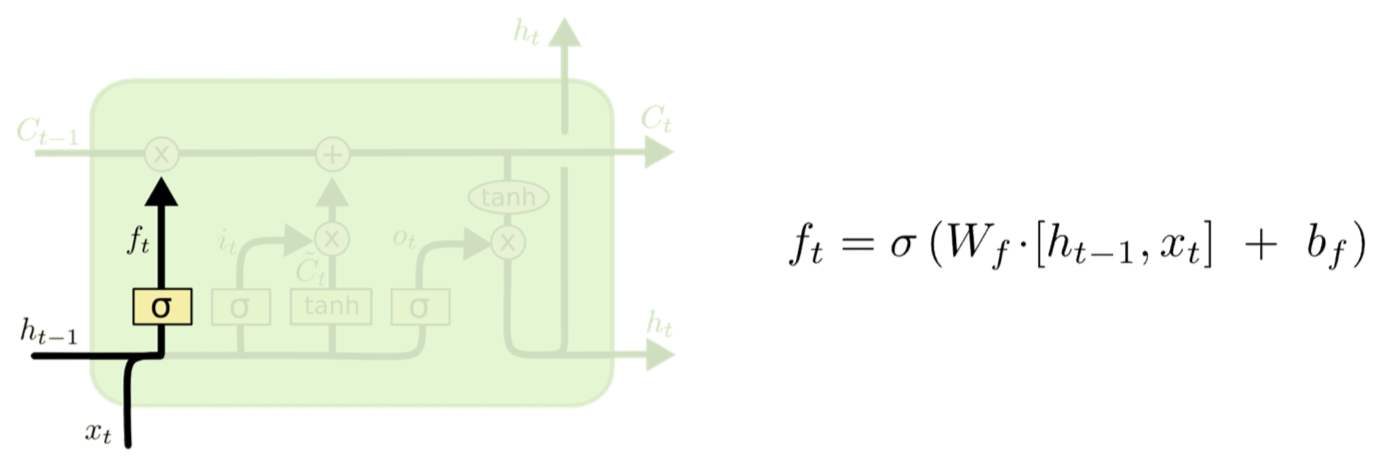
- The first gate determines whether to carry over the history or to forget it
- More precisely, how much of the history to carry over
- Also called the “forget” gate
- Note, we’re actually distinguishing between the cell memory and the state that is coming over time! They’re related though
- Hidden state is compute from memory (which is stored)
Input gate
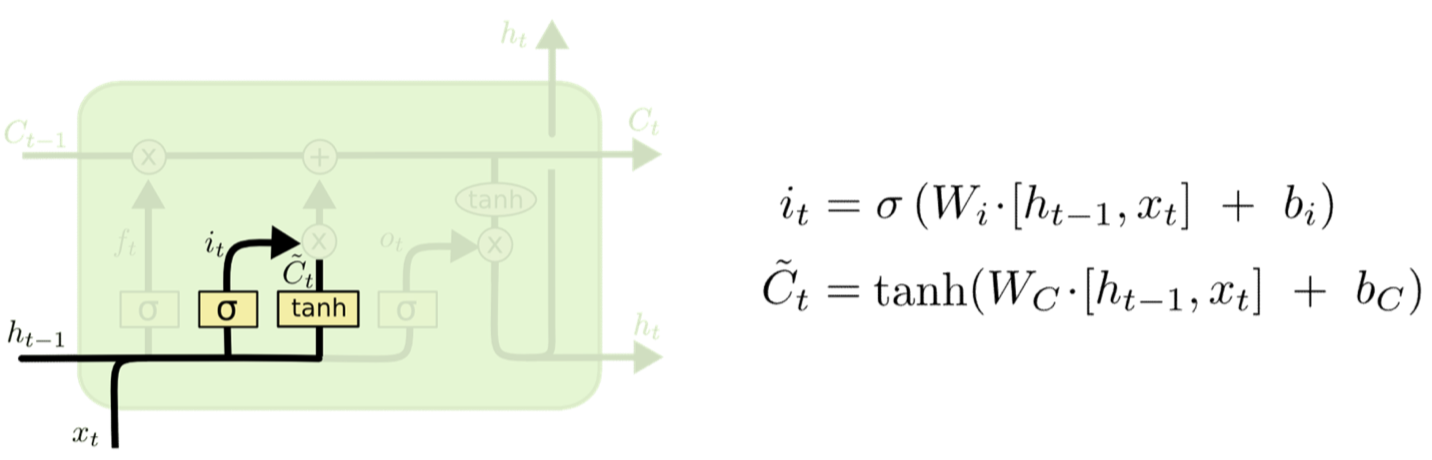
- The second input has two parts
- A perceptron layer that determines if there’s something new and interesting in the input
- 「See a curly brace」
- A gate that decides if its worth remembering
- 「Curly brace is in comment section, ignore it」
- A perceptron layer that determines if there’s something new and interesting in the input
Memory cell update
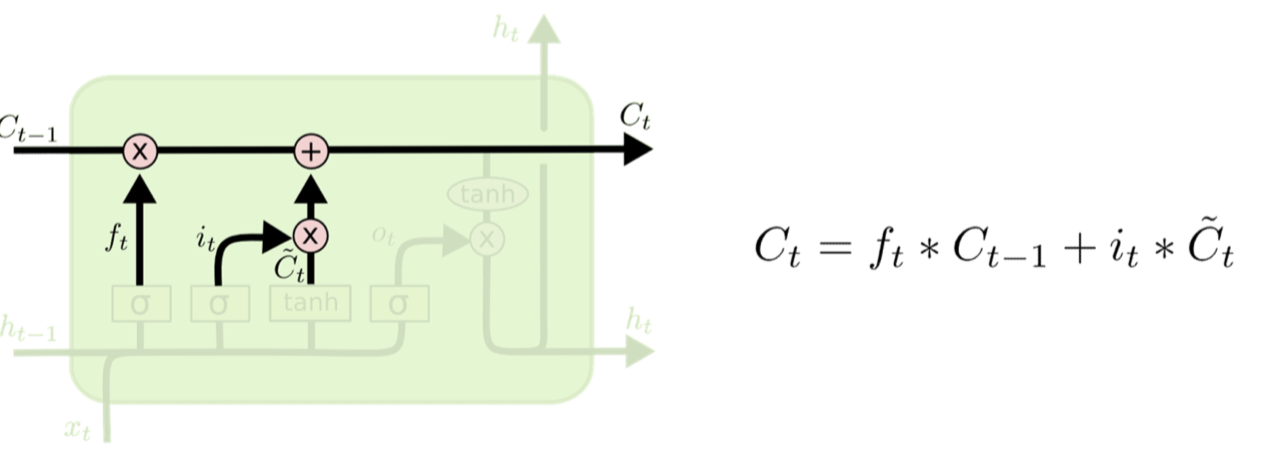
- If something new and worth remembering
- Added to the current memory cell
Output and Output gate
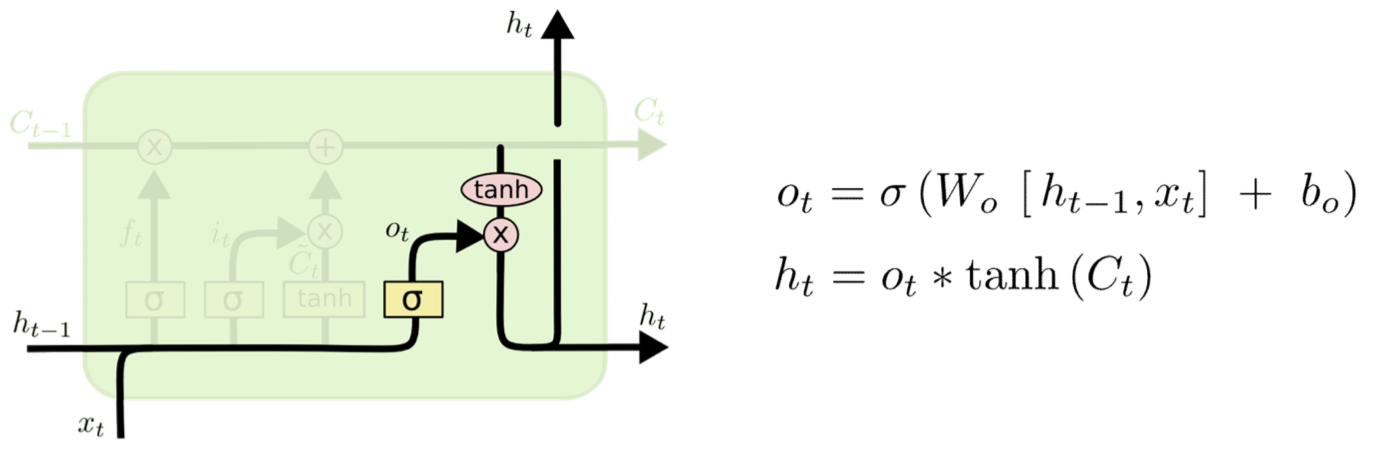
- The output of the cell
- Simply compress it with tanh to make it lie between 1 and -1
- Note that this compression no longer affects our ability to carry memory forward
- Controlled by an output gate
- To decide if the memory contents are worth reporting at this time
- Simply compress it with tanh to make it lie between 1 and -1
The “Peephole” Connection

- The raw memory is informative by itself and can also be input
- Note, we’re using both and
Forward
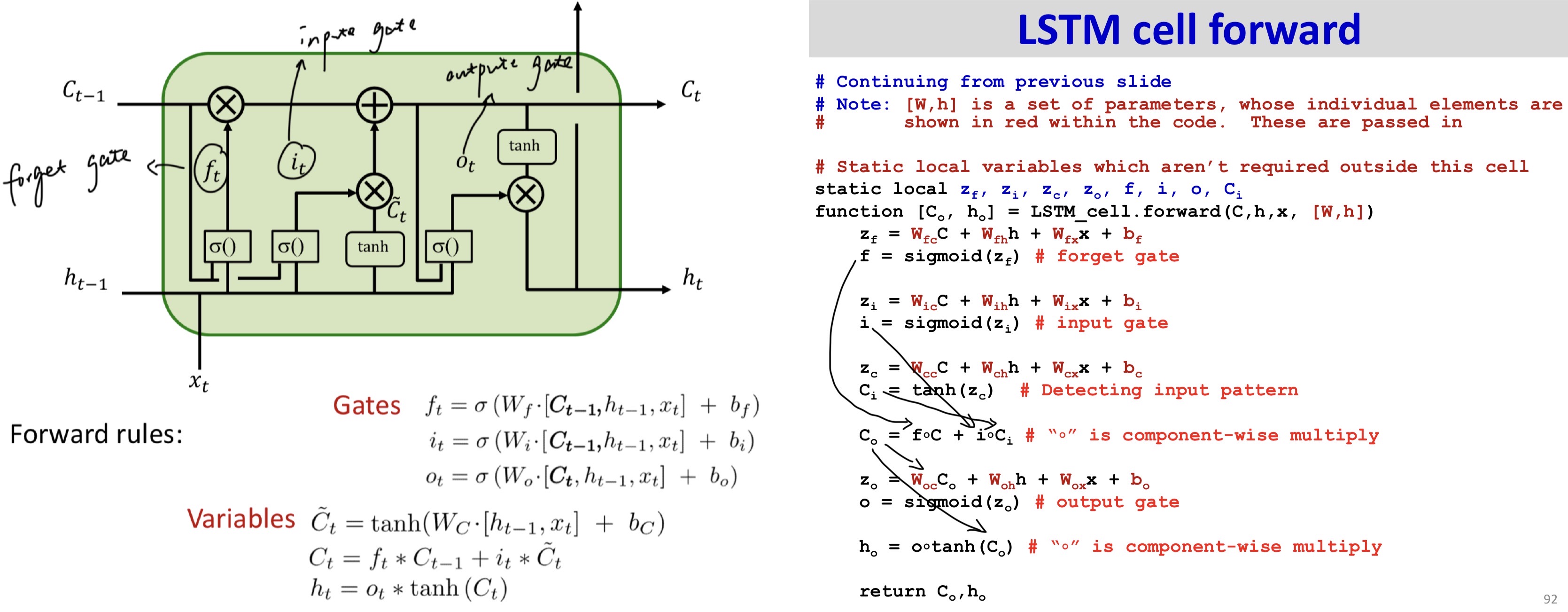
Backward1
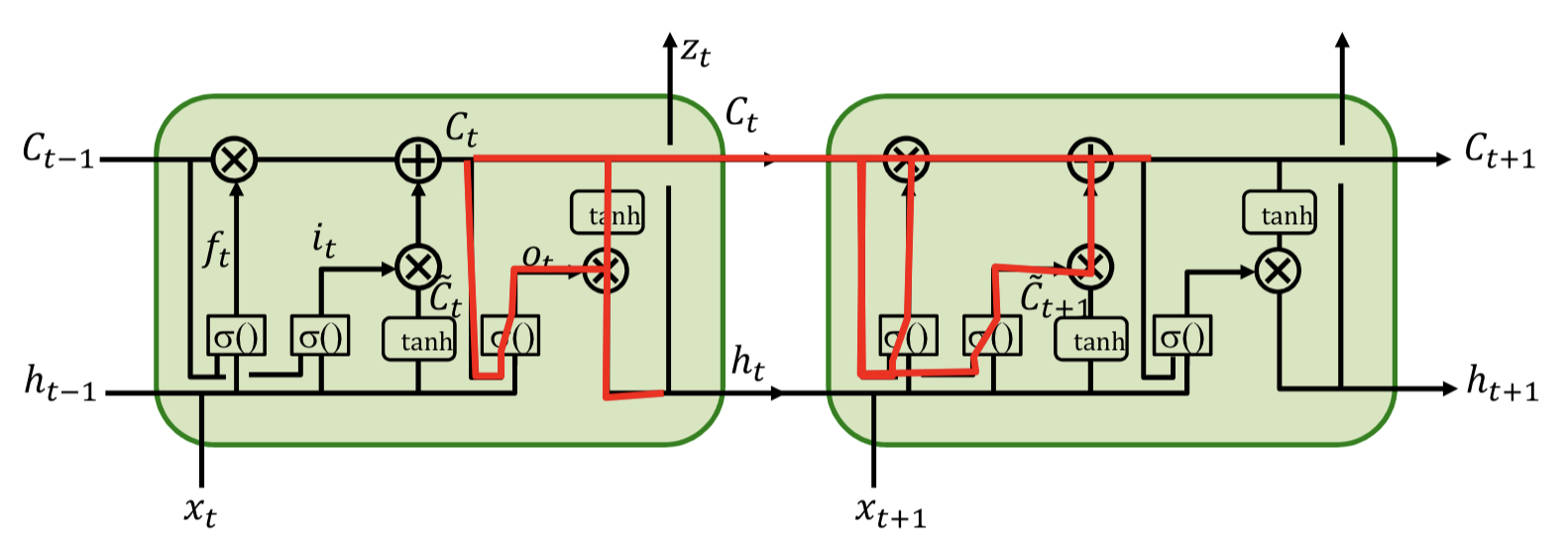
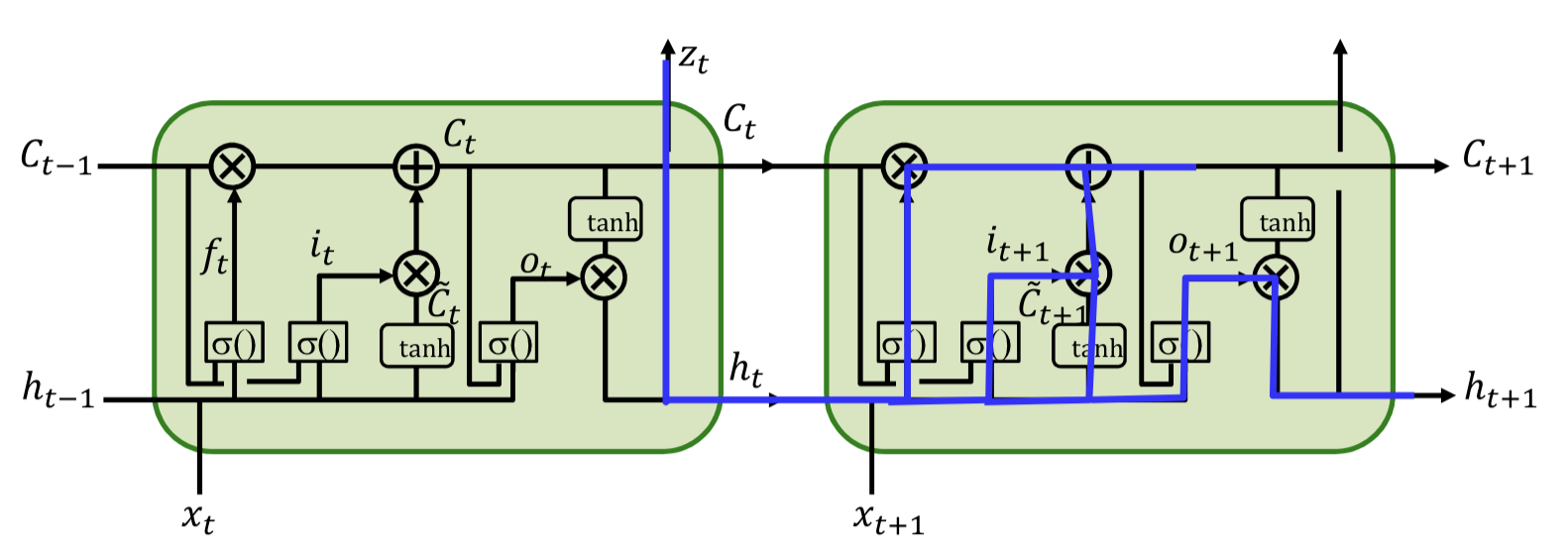 And weights?
And weights?
Gated Recurrent Units
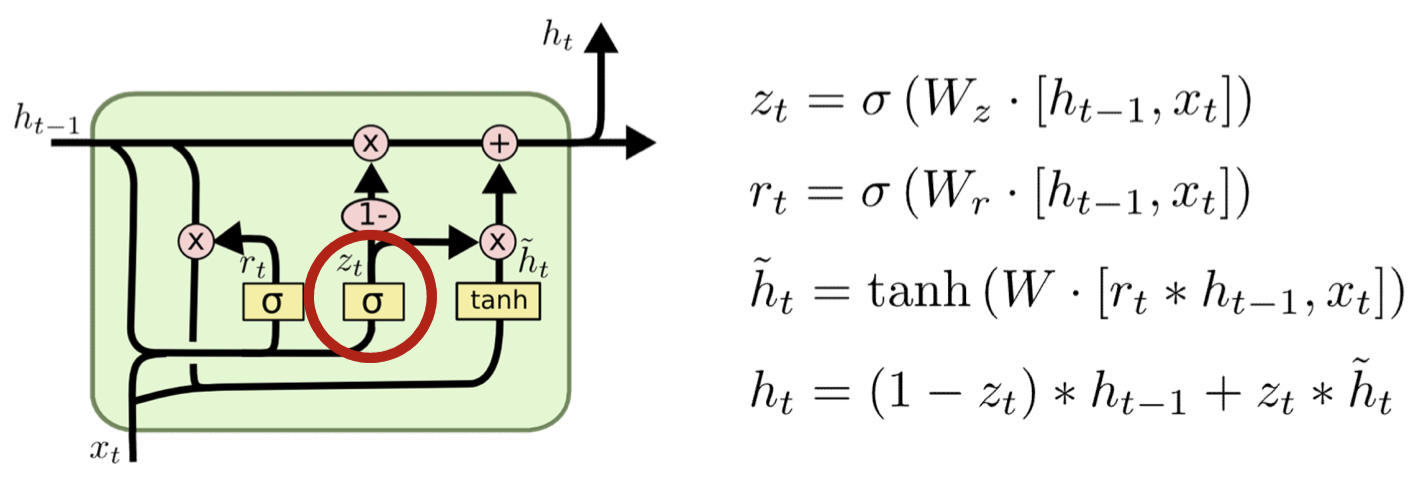
- Combine forget and input gates
- In new input is to be remembered, then this means old memory is to be forgotten
- No need to compute twice
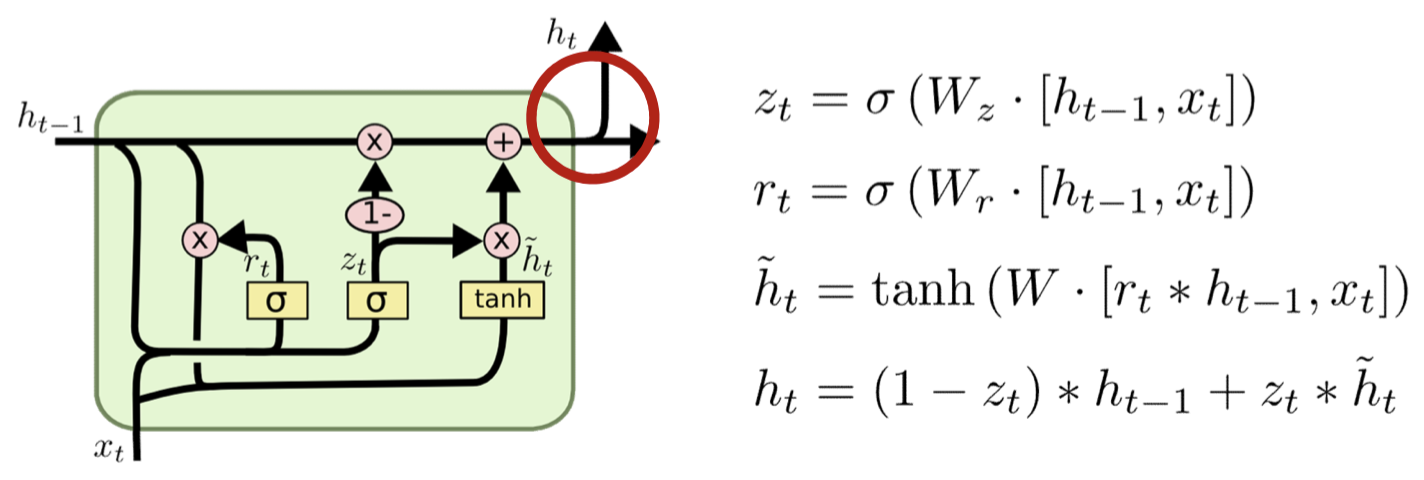
- Don’t bother to separately maintain compressed and regular memories
- Redundant representation
Summary
- LSTMs are an alternative formalism where memory is made more directly dependent on the input, rather than network parameters/structure
- Through a “Constant Error Carousel” memory structure with no weights or activations, but instead direct switching and “increment/decrement” from pattern recognizers
- Do not suffer from a vanishing gradient problem but do suffer from exploding gradient issue
1. http://arunmallya.github.io/writeups/nn/lstm/index.html#/ ↩